👀 정렬이란?
👉 데이터를 순서대로 나열하는 방법을 의미합니다. 정렬은 알고리즘의 굉장히 중요한 주제입니다.
이진탐색을 가능하게도 하고, 데이터를 조금 더 효율적으로 탐색 할 수 있게 만들어 주기 때문입니다!
다음과 같이 책이 꽂혀 있을 때, 가나다 순으로 정렬 해달라는 것을 의미합니다.

숫자로만 이루어진 배열을 오름차순으로 정렬 해보면 다음과 같습니다.
[4, 6, 2, 9, 1] # 정렬되지 않은 배열
[1, 2, 4, 6, 9] # 오름차순으로 정렬된 배열!
[9, 6, 4, 2, 1] # 내림차순으로 정렬된 배열!말로 설명 해보라고 하면 생각보다 설명하기 힘들다는 걸 느낄 수 있습니다!
아래와 같이 컴퓨터에게 정렬을 시키기 위해서는 명확한 과정을 설명 해줘야 합니다.
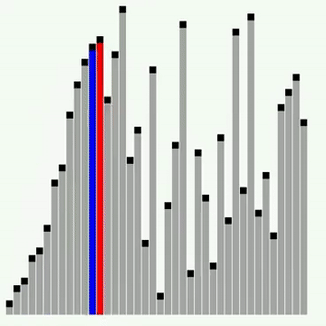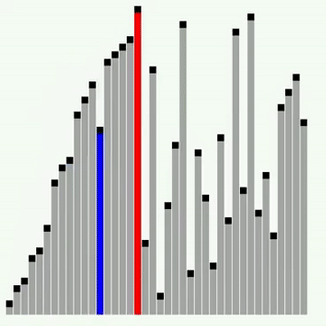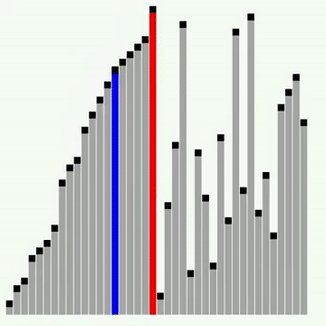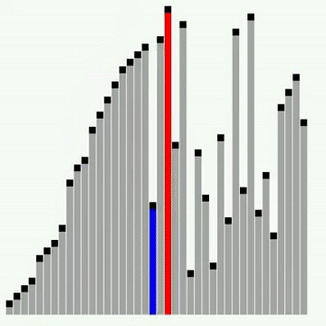
👀 버블정렬이란?
👉 가장 쉽고 직관적인 정렬 방법입니다!
👉 매번 연속된 두 개의 인덱스를 비교하여, 정한 기준의 값을 뒤로 넘겨 정렬하는 방법입니다.
오름차순으로 정렬하고자 한 경우, 비교시마다 큰 값이 뒤로 이동하여 1바퀴를 돌 시 가장 큰 값이 맨 뒤에 저장됩니다.
맨 마지막에는 비교하는 수들 중 가장 큰 값이 저장되기 때문에, (전체 배열의 크기 - 현재까지 순환한 바퀴 수)만큼만 반복하면 됩니다.
첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬하는 방식입니다!
작은 숫자, 큰 숫자 순서로 있으면 내버려두고 큰 숫자, 작은 숫자 순서로 있으면 둘의 위치를 변경하면 됩니다.

👉 기본 로직은 다음과 같습니다.
1) 삽입 정렬은 두 번째 인덱스부터 시작합니다. 현재 인덱스 값과 바로 이전의 인덱스 값을 비교합니다.
2) 만약 이전 인덱스가 더 크면, 현재 인덱스와 바꿔줍니다. (python에서는 a,b = b,a를 사용한다.)
3) 현재 인데스가 더 크면, 교환하지 않고 다음 두 연속된 배열값을 비교합니다.
4) 이를 (전체 배열의 크기 - 현재까지 순환한 바퀴 수)만큼 반복합니다.
👉 이 정렬 알고리즘은 1부터 비교를 시작하여, n-1개, n-2개,...,1개씩 비교를 반복하며,
선택 정렬과 같이 배열이 어떻게 되어 있던 간에 전체 비교를 진행하므로 시간 복잡도는 O(n^2)입니다.
👉 공간복잡도도 이 또한 단 하나의 배열에서만 진행하므로 O(n)입니다.
👀 선택 정렬이란?
👉 이름에서 알 수 있듯이 선택해서 정렬한다라고 생각하시면 됩니다.
다음과 같이 사람들이 일렬로 쭉~ 서 있는 데,
한번 쓱 둘러보면서 가장 키가 작은 사람을 찾습니다.
그리고 전부 다 봤다면, 그 중 가장 키가 작은 사람을 맨 앞으로 오도록 하고
다음에 또 둘러본다음 두번째로 키가 작은 사람을 두번째에 배치 시킵니다.

👉 선택 정렬은 이름에 맞게 현재 위치에 들어갈 값을 찾아 정렬하는 배열입니다.
현재 위치에 저장될 값의 크기가 작냐, 크냐에 따라 최소 선택 정렬과 최대 선택 정렬로 구분 할 수 있습니다.
최소 선택 정렬은 오름차순으로 정렬한 것을 말하고, 최대 선택 정렬은 내림차순으로 정렬된 것입니다.
👉 기본 로직은 다음과 같습니다.
1) 정렬 되지 않은 인덱스의 맨 앞에서 부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아간다.
(정렬되지 않은 인덱스의 맨 앞은, 초기 입력에서는 배열의 시작 위치일 것이다.)
2) 가장 작은 값을 찾으면, 그 값을 현재 인덱스의 값과 바꿔준다.
3) 다음 인덱스에서 위 과정을 반복해준다.
👉 이 정렬 알고리즘은 n-1개, n-2개,...,1개씩 비교를 반복한다.
배열이 어떻게 되어 있던간에 전체 비교를 진행하므로 시간 복잡도는 O(n^2)이다.
👉 공간 복잡도는 단 하나의 배열에서만 진행하므로 O(n)이다.
👀 삽입 정렬이란?
👉 선택 정렬과는 조금 느낌이 다릅니다
선택 정렬이 전체에서 최솟값을 '선택'하는 거라면
삽입 정렬은 전체에서 하나씩 올바른 위치에 '삽입'하는 방식입니다.
선택 정렬은 현재 데이터의 상태와 상관없이 항상 비교하고 위치를 바꾸지만
삽입 정렬은 필요할 때만 위치를 변경하므로 더 효율적인 방법입니다.
이미 키 순으로 정렬된 사람들이 일렬로 쭉~ 서 있는데,
다음 원소가 그 정렬된 사람들 사이를 비집고 들어가면서
아 여기가 내 자리구나! 하면서 삽입하며 정렬하는 방식입니다.

👉 삽입 정렬은 현재 위치에서, 그 이하의 배열들을 비교하여 자신이 들어갈 위치를 찾아, 그 위치에 삽입하는 알고리즘입니다.
👉 기본 로직은 다음과 같다.
1) 삽입 정렬은 두 번째 인덱스부터 시작한다. 현재 인덱스는 별도의 변수에 저장해두고, 비교 인덱스를 (현재 인덱스-1)로 잡는다.
2) 별도로 저장해 둔 삽입을 위한 변수와 비교 인덱스의 배열 값을 비교한다.
3) 삽입 변수의 값이 더 작으면 현재 인덱스로 현재 인덱스의 값을 저장 해주고, 비교 인덱스를 -1하여 비교를 반복한다.
4) 만약 삽입 변수가 더 크면, 비교 인덱스+1에 삽입 변수를 저장한다.
👉 이 정렬 알고리즘 또한 최악의 경우(역으로 정렬 되어 있을 경우)엔 n-1개, n-2개,..,1개씩 비교를 반복하여 시간 복잡도는 O(n^2)이지만, 이미 정렬되어 있는 경우에는 한번씩 밖에 비교를 하지 않아 시간 복잡도는 O(n)이다.
하지만 상한을 기준으로 하는 Big-O notation은 최악의 경우를 기준으로 평가하기 때문에 삽입 정렬의 시간 복잡도는 O(n^2)이다.
👉 공간 복잡도는 단 하나의 배열에서만 진행하므로 O(n)이다.

알고리즘 종류 정리 사이트
https://hsp1116.tistory.com/33
기본 정렬 알고리즘(Sorting Algoritm) 요약 정리 (선택, 삽입, 버블, 합병, 퀵) v1.1
정렬 알고리즘은 n개의 숫자가 입력으로 주어졌을 때, 이를 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘이다. 예를 들어 n개의 숫자가 저장되어있는 배열을, 오름차순의 조건으로
hsp1116.tistory.com
추가로 참고하면 좋을만한 사이트
기본 정렬 알고리즘의 종류와 정리
최종수정일자 : 2020-01-03 이 글은 이미 공부 했었으나, 정렬을 쉽게 정리하지 못하는 사람을 위해 정리하였다. 정렬의 종류도 많으며, 설명하기가 쉽지 않다. 동작은 다양하며, 머리속에 어렴풋이
roka88.dev
'⛵ 항해 중 > 알고 보면 알기 쉬운 알고리즘' 카테고리의 다른 글
| 해쉬 - 해쉬 테이블, 해쉬 함수, 체이닝, 개방 주소법 (0) | 2021.11.13 |
|---|---|
| 스택, 큐 (0) | 2021.11.13 |
| 재귀함수 - 팩토리얼, 회문 검사 (0) | 2021.11.13 |
| 이진 탐색, 순차 탐색 (0) | 2021.11.13 |
| 클래스, 객체, 생성자, 메소드 (0) | 2021.11.13 |




댓글