👀 그래프란?
👉 연결되어 있는 정점과 정점 간의 관계를 표현 할 수 있는 자료구조
저번에 트리를 배우면서 배웠던 "비선형 구조" 에 대해 기억 나시나요?
비선형 구조는 표현에 초점이 맞춰져 있다고 말씀 드렸는데,
선형구조는 자료를 저장하고 꺼내는 것에 초점이 맞춰져 있고,
비선형구조는 표현에 초점이 맞춰져 있습니다.
그래프는 바로 연결 관계에 초점이 맞춰져 있습니다.
페이스북을 예시로 들어볼게요!
제가 친구 "제니"를 알고 있고, "로제"와 친합니다.
그리고 "로제"는 트와이스 "사나"를 안다고 하면,
저는 "사나"와 2촌 관계라고 말할 수 있겠죠!

👀 그래프에서 사용되는 용어
👉 노드(Node): 연결 관계를 가진 각 데이터를 의미합니다. 정점(Vertex)이라고도 합니다
👉 간선(Edge): 노드 간의 관계를 표시한 선
👉 인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)
예를 들어 표현 해보자면

👀 추가적으로 그래프는 유방향 그래프와 무방향 그래프가있습니다.
👉 유방향 그래프(Directed Graph): 방향이 있는 간선을 갖습니다.
간선은 단방향 관계를 나타내며, 각 간선은 한 방향으로만 진행할 수 있습니다.
👉 무방향 그래프(Undirected Graph)는 방향이 없는 간선을 갖습니다

👀 그래프의 표현방법은?
그래프라는 개념을 컴퓨터에서 표현하는 방법으로는 두가지가 있습니다.
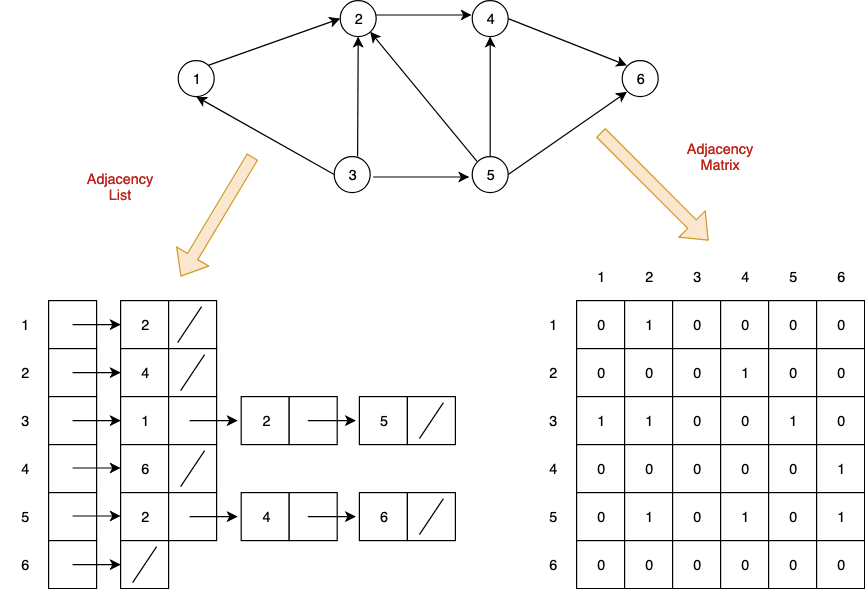
👉 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현
👉 인접 리스트(Adjacnecy List) : 링크드 리스트로 그래프의 연결 관계를 표현

👀 인접 행렬 vs 인접 리스트의 차이점은?
👉 바로 시간 vs 공간입니다.
👉 인접 행렬로 표현하면 즉각적으로 0과 1이 연결되었는지 여부를 바로 알 수 있습니다.
그러나, 모든 조합의 연결 여부를 저장해야 되기 때문에 O(노드^2) 만큼의 공간을 사용해야 합니다.
👉 인접 리스트로 표현하면 즉각적으로 연결되었는지 알 수 없고, 각 리스트를 돌아봐야 합니다.
따라서 연결되었는지 여부를 알기 위해서 최대 O(간선) 만큼의 시간을 사용해야 합니다.
대신 모든 조합의 연결 여부를 저장할 필요가 없으니 O(노드 + 간선) 만큼의 공간을 사용하면 됩니다.
👀 DFS & BFS란?
👉 자료의 검색, 트리나 그래프를 탐색하는 방법.
👉 한 노드를 시작으로 인접한 다른 노드를 재귀적으로 탐색하고 끝까지 탐색하면 다시 위로 와서 다음을 탐색하여 검색하는 방법
한 노드를 시작으로 인접한 모든 정점들을 우선 방문하는 방법.
더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 넓이 우선 검색을 적용한다.
❓ 그 전에! 왜 DFS & BFS 를 배울까요?
👉 정렬된 데이터를 이분 탐색하는 것처럼 아주 효율적인 방법이 있는 반면에,
모든 경우의 수를 전부 탐색해야 하는 경우도 있습니다
❓ 대표적인 예시가 알파고입니다.
대국에서 발생하는 모든 수를 계산하고 예측해서 최적의 수를 계산해내기 위해 모든 수를 전부 탐색해야 합니다.
👀 DFS와 BFS의 차이점은?
👉 탐색하는 순서에서 차이가 있습니다.
👉 DFS 는 하나를 끝까지 파고드는 것이고,
👉 BFS 는 갈라진 모든 경우의 수를 탐색해보는 점에서 차이점이 있습니다.

👀 DFS는?
👉 끝까지 파고드는 것이라, 그래프의 최대 깊이 만큼의 공간을 요구합니다.
따라서 공간을 적게 씁니다. 그러나 최단 경로를 탐색하기 쉽지 않습니다.
👀 BFS는?
👉 최단 경로를 쉽게 찾을 수 있습니다!
모든 분기되는 수를 다 보고 올 수 있으니까요.
그러나, 모든 분기되는 수를 다 저장하다보니 공간을 많이 써야하고,
모든 걸 다 보고 오다보니 시간이 더 오래걸릴 수 있습니다.
'항해 중 > 알고 보면 알기 쉬운 알고리즘' 카테고리의 다른 글
| 힙 - 원소 추가하기, 원소 삭제하기 (0) | 2021.11.14 |
|---|---|
| 트리 - 이진 트리, 완전 이진 트리 (0) | 2021.11.14 |
| 해쉬 - 해쉬 테이블, 해쉬 함수, 체이닝, 개방 주소법 (0) | 2021.11.13 |
| 스택, 큐 (0) | 2021.11.13 |
| 정렬 - 버블정렬, 선택정렬, 삽입정렬 (0) | 2021.11.13 |




댓글